Among many in-house developed scripts and programs of the whole GOP orbit determination system, the Bernese GPS Software (Dach et al., 2007) is the core analysing tool for batch processing of double-difference GNSS observations. Our system has been developed as highly efficient based on pre-processing of the last 6 hours followed by the combination with preceding solutions. For the combination, the Bernese GPS software was modified to support a stacking of orbit arcs from sub-daily solutions. Only the GNSS navigation messages and observation and predicted Earth rotation parameters (ERPs) are needed to initiate the procedure. Through analysing navigation messages, we are also able to detect satellite manoeuvres, which is important in the pre-processing steps. In order to provide overall robustness, our solution consists of two orbit improvements (Fig 2) wherefore either predicted precise IGS orbits or broadcast orbits could be then used as a priori orbit information

Pre-processing is the main part of each of the two solution iterations. All steps are efficiently performed in five individual clusters in parallel (Fig 1, black boxes). In all the steps, where the least square adjustment (LSQ) is applied (GPSxxx), a full normal equation matrix (NEQ) is saved as the result. It is followed by the NEQ combination applying sequential LSQ – a) COMB_CLU step combines cluster-NEQs into a 6-hour global solution and b) COMB_SEQ step combines 6-hour global-NEQs into a daily solution. The latter is the product of the pre-processing and orbit improvement iteration step. After the second orbit improvement step is completed, the 6-hour NEQs are combined into a single 3-day final orbit product using different variants (Fig 2, bottom three blocks). The orbit parameters (as well as the ERPs and coordinates) are stacked there for an interval of 3 days in order to provide the best 24h orbit prediction as the final product. The parameterization of final 3-day orbit model is a key part of the precise orbit prediction and thus the procedure will be briefly addressed, too.
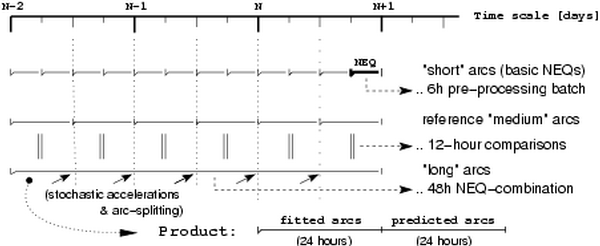
In the best case, the six initial orbit parameters plus nine additional solar radiation parameters of the extended CODE model (Springer et al, 1999) are combined into a unique orbit arc over a 3-day interval. For various reasons like satellite manoeuvres, eclipsing events or data loss, the existing orbit model is not always satisfactory and the solution then does not provide the best results. The iterative procedure is provided in order to handle the best setup of the orbit parameters. The main goal is to identify the epoch, at which the individual satellite orbit arc should either be split into two (or more) pieces, or at which additional stochastic parameters representing a satellite velocity should be introduced. To recognize such epochs, the long orbit arc of every satellite is compared with the original short one as shown in Fig 3. The information about the satellite manoeuvre, obtained at the initial phase of the processing, is used in this procedure too.